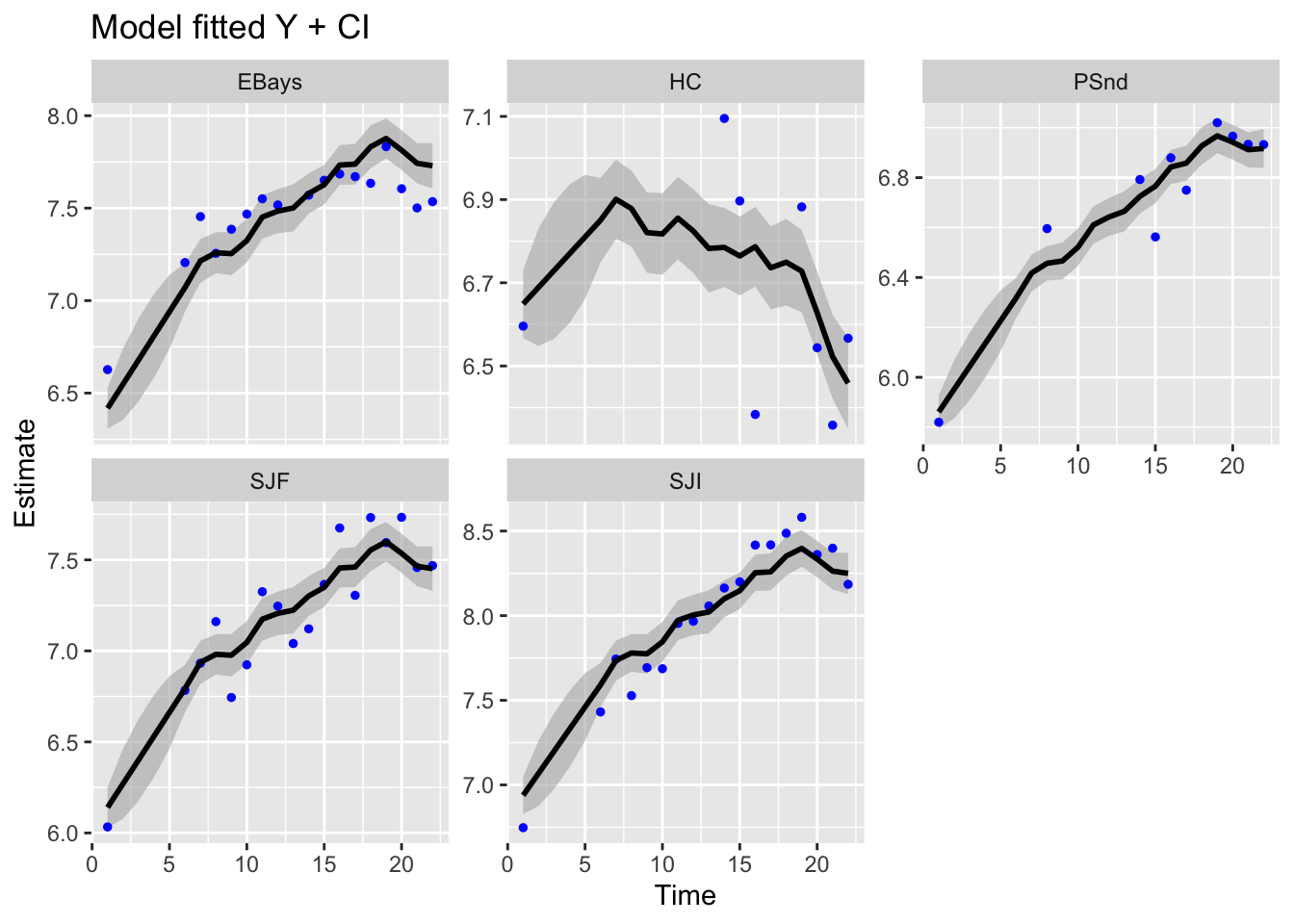
8.3 Different time series observing a RW
The three outer regions (EBays, SJI, and SJF) are observing one random walk and PSnd and HC (more interior) are each observing their own. The regions are correlated. The observations error variances are shared within regions but unique across regions. \[\begin{equation} \begin{gathered} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}_t = \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}_{t-1} + \begin{bmatrix}u_1\\u_2\\u_3\end{bmatrix} + \begin{bmatrix}w_1\\ w_2\\ w_3\end{bmatrix}, \textrm{ } \mathbf{w}_t \sim \,\text{MVN}\begin{pmatrix}\begin{bmatrix}0\\0\\0\end{bmatrix}, \begin{bmatrix}q_1&c_{12}&c_{13}\\c_{12}&q_2&c_{23}\\c_{13}&c_{23}&q_3\end{bmatrix} \end{pmatrix}\\ \begin{bmatrix}y_1\\y_2\\y_3\\y_4\\y_5\end{bmatrix}_t = \begin{bmatrix}1&0&0\\1&0&0\\1&0&0\\0&1&0\\0&0&1\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}_t + \begin{bmatrix}0\\a_2\\a_3\\0\\0\end{bmatrix} + \begin{bmatrix}v_1\\ v_2\\ v_3 \\ v_4 \\ v_5\end{bmatrix}, \textrm{ } \mathbf{v}_t \sim \,\text{MVN} \begin{pmatrix} \begin{bmatrix}0\\0\\0\\0\\0\end{bmatrix}, \begin{bmatrix} r_1&0&0&0&0\\ 0&r_1&0&0&0\\ 0&0&r_1&0&0\\ 0&0&0&r_2&0\\ 0&0&0&0&r_3 \end{bmatrix} \end{pmatrix} \end{gathered} \tag{8.4} \end{equation}\]
Create set up the model:
Q <- "unconstrained"
R <- matrix(list(0), 5, 5)
diag(R) <- c("Outer", "Outer", "Outer", "PSnd", "HC")
Z <- matrix(0, 5, 3)
colnames(Z) <- c("Outer", "PSnd", "HC")
Z[1:3, 1] <- 1
Z[4, 2] <- Z[5, 3] <- 1Fit with MARSS():
yt <- t(harborSealWA)[2:6, ]
fit <- MARSS(yt, model = list(R = R, Q = Q, Z = Z))plot.pars(fit)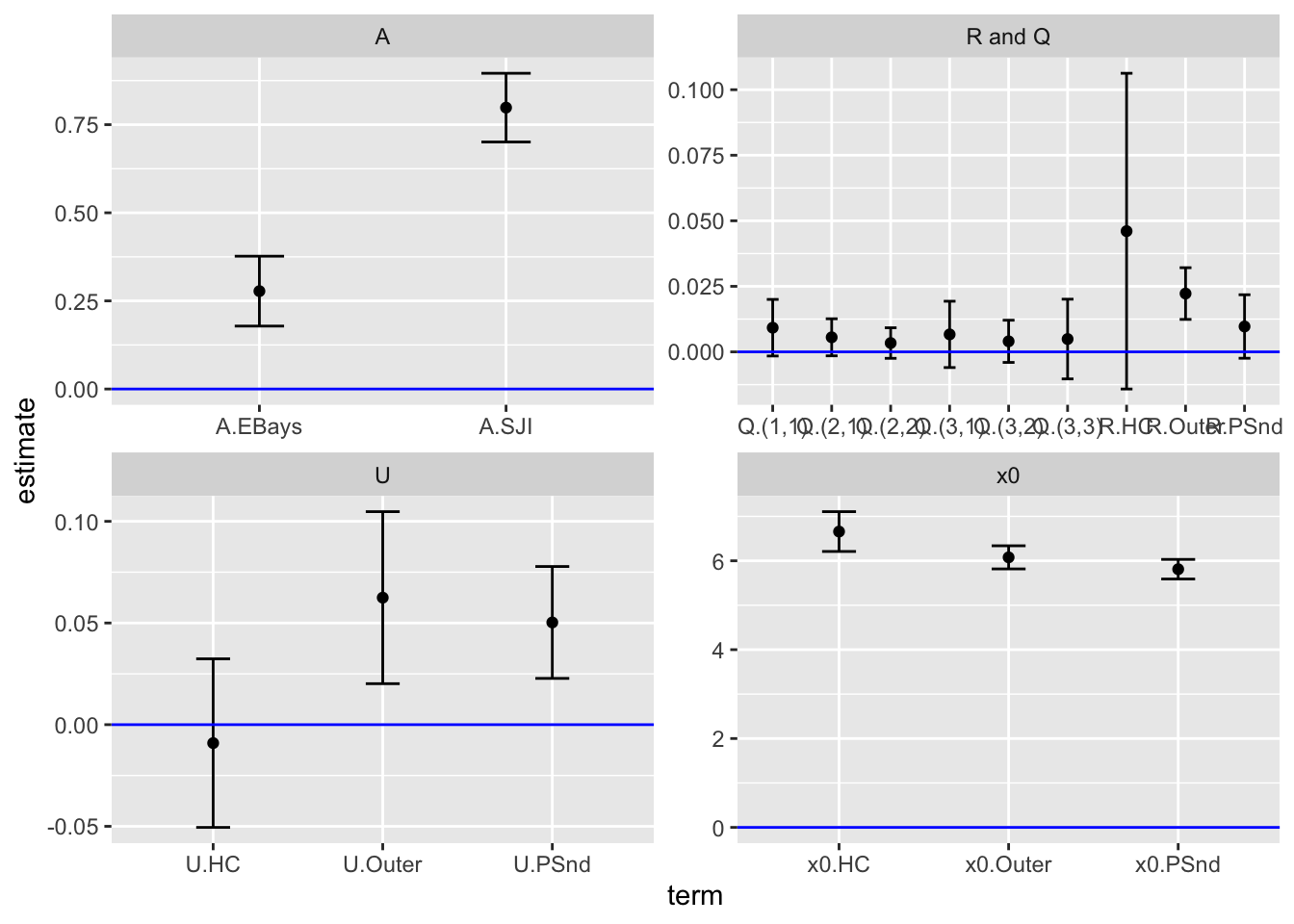
Model fits.
ggplot2::autoplot(fit, plot.type = "model.ytT")