8.2 Multiple time series each observing a RW

Each time series is observing its own random walk but the random walks have correlated process error. \[\begin{equation} \begin{gathered} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}_t = \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}_{t-1} + \begin{bmatrix}u_1\\u_2\\u_3\end{bmatrix} + \begin{bmatrix}w_1\\ w_2\\ w_3\end{bmatrix}, \textrm{ } \mathbf{w}_t \sim \,\text{MVN}\begin{pmatrix}\begin{bmatrix}0\\0\\0\end{bmatrix}, \begin{bmatrix}q_1&c_{12}&c_{13}\\c_{12}&q_2&c_{23}\\c_{13}&c_{23}&q_3\end{bmatrix} \end{pmatrix}\\ \begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix}_t = \begin{bmatrix}1&0&0\\0&1&0\\1&0&0\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}_t + \begin{bmatrix}0\\0\\0\end{bmatrix} + \begin{bmatrix}v_1\\ v_2\\ v_3\end{bmatrix}, \textrm{ } \mathbf{v}_t \sim \,\text{MVN}\begin{pmatrix}\begin{bmatrix}0\\0\\0\end{bmatrix},\begin{bmatrix}r&0&0\\0&r&0\\0&0&r\end{bmatrix} \end{pmatrix} \end{gathered} \tag{8.3} \end{equation}\]

Create set up the model:

Q <- "unconstrained"
R <- "diagonal and equal"

Fit with MARSS():

fit <- MARSS(yt, model = list(R = R, Q = Q))

plot.pars(fit)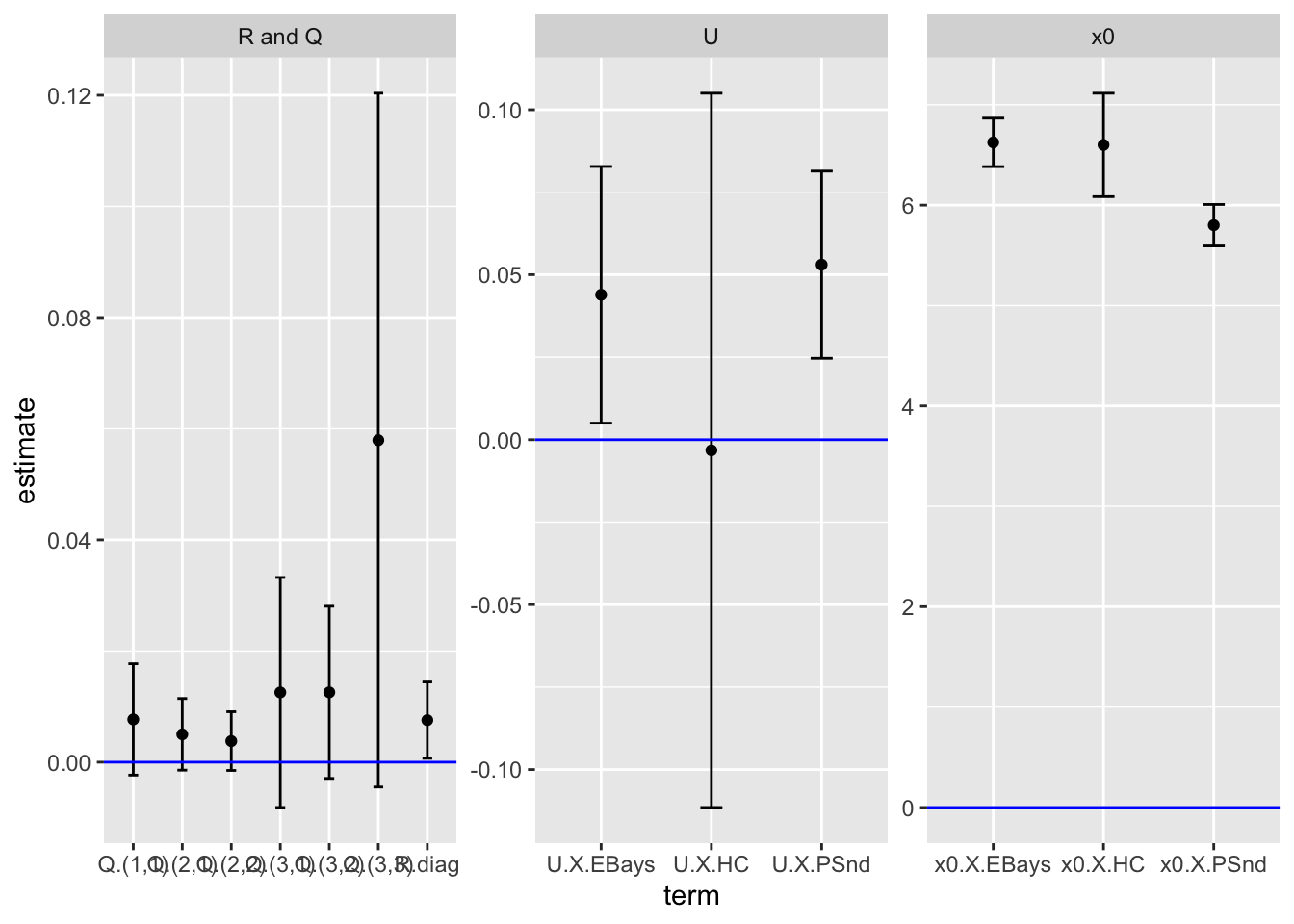

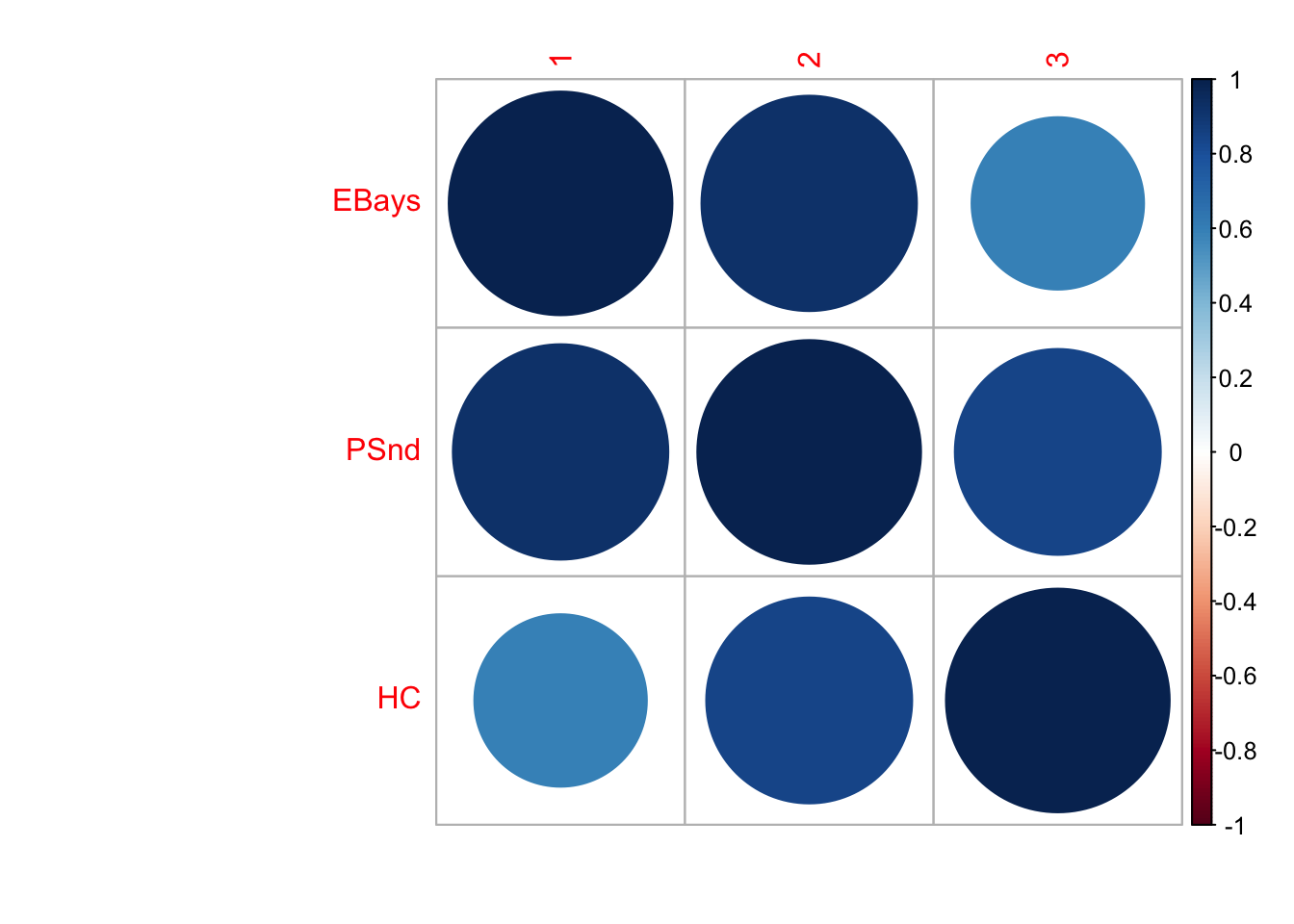
Look at the \(\mathbf{Q}\). Hood Canal (HC) appears to be behaving independently.

Q.est <- coef(fit, type = "matrix")$Q
rownames(Q.est) <- rownames(yt)
corrplot::corrplot(cov2cor(Q.est))